親が家庭でこどもに算数の初歩を教えてあげるのは、非常に重要なことです。しかし、順序だてて教えていかないと、高学年へ進んだときに計算嫌いな子になってしまうかもしれません。また、海外に移住した日本人などは、家族の親密度が高くなり、勉強も親が教えなければならない場面も増えていきます。そんなときに、覚えが悪いからなどと言って声を荒げたり、手を出したりと子供に強く当たると、勉強が大嫌いな子になってしまうかもしれません。
本記事では、子供にどうやって算数の基礎を教えて言えばいいのかという部分のヒントを紹介します。
こどもと一緒に楽しむ
たのしい時間を過ごす工夫をする
・スタンプ帳などを作り、ステージをクリアするごとにスタンプやシールを押してあげる。
・おもしろい発見をしたらスタンプを倍増する
・数あてゲームで夕飯のおかずやおやつを賭ける
・兄弟がいれば点数やスタンプの数を競わせる
・お兄さんやお姉さんがいればそのスタンプ帳や達成時の記念写真などを見せる
などといった工夫をしながらたのしく学習することがだいじです。
時間を決める
「1日30分だけ」とか「1時間だけ」というように時間を決めていっしょに勉強してください。だらだら続けるのはよくありません。
親は絶対的知恵者ではない
よく子供の前ではなんでも知っているかのような顔をして、さもその道の権威であるかのように振い、間違ったことでも平気で教えようとする親がいますが、そういう人は教育者として失格です。
かっこつけなくて良いんです。
わからなければどうやったらわかるのかを話し合ったり、知っている人に真摯に聞く姿勢が大事です。そして一緒に調べ学ぶということが最も重要です
分からないことにぶつかった際の3原則
・知らないことは恥ではない
➔ 知らないことを知らないままにすることが本当の恥ずかしい行為だと教えましょう。
・知っている人に真摯に聞く
➔ 知っている人がいるのなら、メモ帳と鉛筆を持って真摯に聞く姿勢を養いましょう。
・Aiやインターネットを適切に活用する
➔ Aiを使う場合は、思いつく限りどこまでも深堀りして質問し、理解を最大化するように指導しましょう。
質問や調べるときに大事なこと
・人から聞いたことを要約して反芻することで理解が正しかったかを聞いてもらう
➔教えてくれた人への礼儀でもありますね
・調べたり聞いたりしたことはメモに残しておく
➔効果的な情報の整理方法をこどもと話し合ってみる(後述)
・知ったかぶりをしないように教えている親のほうも適当なことを言わない
➔わからないことを真摯に聞けない人こそ恥じるべき人だと教えましょう
・出典を隠さない姿勢
➔情報の出典を隠して、さも自分が発見したかのように発表することは、
剽窃(ひょうせつ)といって、一番やってはいけないことだと教えましょう。
すべてのはじまり:総和が10未満の1桁の足し算
いわゆる1+1みたいな足し算ですが、これを桁上がりしない1桁の数で足し算する練習です。
質問したら即座に答えられるようになるように練習します。ゲームやカードなどを取り入れて、楽しく勉強する雰囲気をつくってください。
※未満という言葉を教える必要はない。「いっしょに10にならない数をさがそう」で良い。
※親が一緒に参加することが非常に大事です。
※そしてできないからと言って叱ってはいけません!
| 1 | + | 1 | = | 2 |
| 1 | + | 2 | = | 3 |
| 1 | + | 3 | = | 4 |
| 1 | + | 4 | = | 5 |
| 1 | + | 5 | = | 6 |
| 1 | + | 6 | = | 7 |
| 1 | + | 7 | = | 8 |
| 1 | + | 8 | = | 9 |
| 2 | + | 1 | = | 3 |
| 2 | + | 2 | = | 4 |
| 2 | + | 3 | = | 5 |
| 2 | + | 4 | = | 6 |
| 2 | + | 5 | = | 7 |
| 2 | + | 6 | = | 8 |
| 2 | + | 7 | = | 9 |
| 3 | + | 1 | = | 4 |
| 3 | + | 2 | = | 5 |
| 3 | + | 3 | = | 6 |
| 3 | + | 4 | = | 7 |
| 3 | + | 5 | = | 8 |
| 3 | + | 6 | = | 9 |
| 4 | + | 1 | = | 5 |
| 4 | + | 2 | = | 6 |
| 4 | + | 3 | = | 7 |
| 4 | + | 4 | = | 8 |
| 4 | + | 5 | = | 9 |
| 5 | + | 1 | = | 6 |
| 5 | + | 2 | = | 7 |
| 5 | + | 3 | = | 8 |
| 5 | + | 4 | = | 9 |
| 6 | + | 1 | = | 7 |
| 6 | + | 2 | = | 8 |
| 6 | + | 3 | = | 9 |
| 7 | + | 1 | = | 8 |
| 7 | + | 2 | = | 9 |
| 8 | + | 1 | = | 9 |
目標
この練習の目標は、上に挙げたすべての足し算の組み合わせを即座に答えられるようにすることです。クイズ形式で楽しくやってみてください。丸暗記などを強要してはぜったいにいけません。たのしくゲーム感覚で覚えさせます。きっと毎日やっても数週間かかると思います。
こんな工夫も取り入れよう
「〇と□を足したら答えは何?」のような質問に加えて、例えば、「2に何を足すと9になる?」のような質問や次のようなゲームをしてみます。
数当てゲーム
- 「おとうさん(おかあさん)が思った数字の足し算を当ててね」と言い、次いで「わからなかったらヒントくださいと言ってね」と言います。
- なにもヒントが無ければわかりません。もしもこどもが間違った答えをあてずっぽうに言った場合は、間違っている旨を伝えて、「あと何回間違えたら、今日のおやつをもらうぞー」など、子供から笑いをとってください。間違ったことを言った場合は、最後に必ず「わからなかったらヒントくださいと言ってね」と言います。
- カウントダウンしながら切迫感を出すのも面白いです。
- もしも子供が言った数字が偶然にも思った数式のなかに入って入れば、どこに入っていたか教えてあげます。
- ヒントをくださいと言われたら「一番左の数字は3」のように、式のなかで明確になっていないところを教えてあげます。
- このようにして足しても桁上りしない数の足し算を完成させます。
- たとえば「晩ご飯のおかずから嫌いなものを1つだけ指定できる権利」などを賭けてゲーム性を持たせるのも面白いです。
こどもの発見を褒めたたえよう
子供が何かの法則性に気が付いたらほめてあげる。
・左辺の数字が大きくなっていく毎に、右辺に置くことができる数字が少なくなっていく
・左辺の数字が大きくなっていく毎に、答えの数字の開始の数が大きくなっていく
・9の場合はあてはまる式が1つもない
など。なんでもいい。
子供がなにかを発見したら、スタンプを多めに押す、褒めたたえる、食事のときに家族全員で乾杯するなどをしてあげる。
※何も気づかなくても構わない。発見を強要したり、発見をしないからといって怒ったりしないことが大事。
10の補数
算数を教えるうえで非常に重要な概念が「10の補数」です。子供にはこの「10の補数」という言葉を教える必要はありません。10の補数とは、「ある1桁の数字 にあと何を足したら10になるか」という数です。
ヒント
7に何をたすと10になる? ➔ 3
4に何をたすと10になる? ➔ 6
クイズ形式でたのしくやってみてください。
即座に応えられるようになるまで、総和が10未満の1桁の足し算の練習などを混ぜながらやってみてください。
目標
即座に答えが言えるようになるまで続けます。
便利グッズの紹介
数字の計算をするときに暗算に頼らず、実際のおはじきで見せながら学習するときに便利です。

おはじきセット
https://amzn.to/4mCzdIC
桁上りのある1桁の足し算
次は、「桁上りのある1桁の足し算」です。
これは下記のような計算です。
| 1 | + | 9 | = | 10 |
| 2 | + | 8 | = | 10 |
| 2 | + | 9 | = | 11 |
| 3 | + | 7 | = | 10 |
| 3 | + | 8 | = | 11 |
| 3 | + | 9 | = | 12 |
| 4 | + | 6 | = | 10 |
| 4 | + | 7 | = | 11 |
| 4 | + | 8 | = | 12 |
| 4 | + | 9 | = | 13 |
| 5 | + | 5 | = | 10 |
| 5 | + | 6 | = | 11 |
| 5 | + | 7 | = | 12 |
| 5 | + | 8 | = | 13 |
| 5 | + | 9 | = | 14 |
| 6 | + | 4 | = | 10 |
| 6 | + | 5 | = | 11 |
| 6 | + | 6 | = | 12 |
| 6 | + | 7 | = | 13 |
| 6 | + | 8 | = | 14 |
| 6 | + | 9 | = | 15 |
| 7 | + | 3 | = | 10 |
| 7 | + | 4 | = | 11 |
| 7 | + | 5 | = | 12 |
| 7 | + | 6 | = | 13 |
| 7 | + | 7 | = | 14 |
| 7 | + | 8 | = | 15 |
| 7 | + | 9 | = | 16 |
| 8 | + | 2 | = | 10 |
| 8 | + | 3 | = | 11 |
| 8 | + | 4 | = | 12 |
| 8 | + | 5 | = | 13 |
| 8 | + | 6 | = | 14 |
| 8 | + | 7 | = | 15 |
| 8 | + | 8 | = | 16 |
| 8 | + | 9 | = | 17 |
| 9 | + | 1 | = | 10 |
| 9 | + | 2 | = | 11 |
| 9 | + | 3 | = | 12 |
| 9 | + | 4 | = | 13 |
| 9 | + | 5 | = | 14 |
| 9 | + | 6 | = | 15 |
| 9 | + | 7 | = | 16 |
| 9 | + | 8 | = | 17 |
| 9 | + | 9 | = | 18 |
計算の方法
- 「X + Y = Z」という計算になります(こどもに言う必要はありません)
- このXとYとでどちらが大きい数字かを言わせます
- 大きい方の数字の10の補数を答えさせます、
例として8+3の場合を考えると、
8+3だと8のほうが大きいので、
「8になにを足したら10になるかな?」などと聞きます。
8の10の補数は2です。
この2は「8+3」の3を(1+2)のように分解してもってきます。
これで10を1つ作ることができたことを教えます。 - 小さいほうの数字(この場合3)から2を引くかたちで分解した数(1+2)を答えさせる。
2は8を10にするために(8+3)の3から分解して持ってきたので、
のこりの1と10を足して答え(11)を出します。 - おはじきや電卓などを使って答えが正しいことを確認します
※このように数字を分解して計算する方法を「さくらんぼ計算」(後述)と言います。
ヒント
これに関しても、数当てゲームや、クイズや遊びを取り入れながら楽しくやってみてください。
そして、子供が何か法則性など発見したら「ほめて」あげてください。もちろんなにも発見しなくても怒ったりしないでくださいね。
ここで足し算というのは数字を分解してもすべて足せば正しい答えになり、さらに10の補数を先に作ったりしても正しい答えになり、足し算だけなら順番はどうでもすべて足せば答えがちゃんと出ることなどを発見できたら褒めまくってあげてください。
気づきと発見を褒めよう
桁上がりしない1桁の足し算と違って、桁上がりのある1桁の足し算では、1と何かを足す場合のほうが候補が少なく、逆に9と何かを足す場合はすべての数字が当てはまるなどの特徴があります。なんでも良いので子供が発見した法則を大絶賛しましょう。
目標
すらすらと回答できるようになるまでいっしょに勉強してください。
さくらんぼ計算
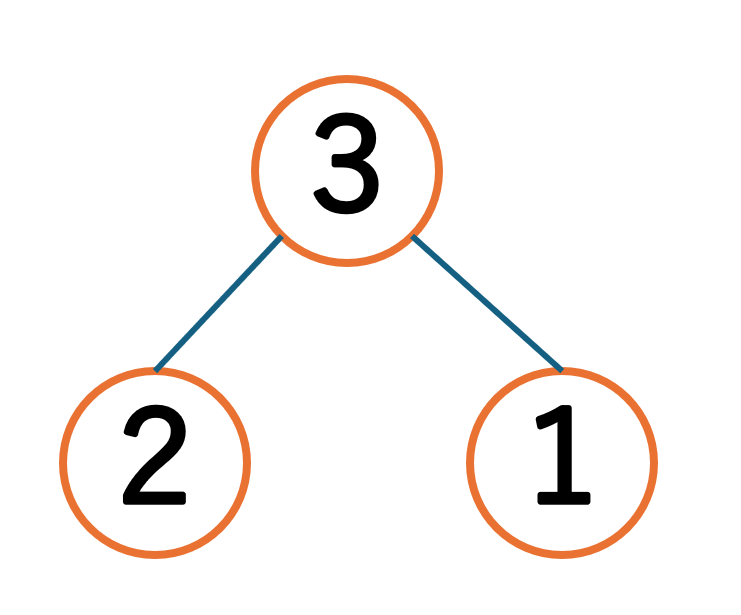
先ほどの例「8+3=11」のような場合に、計算をわかりやすくするための方法の1つが「さくらんぼ計算」です。
「8の10の補数」を作るために「3を2と1」に分解したところです。これがさくらんぼのように見えることから、さくらんぼ計算と言います。
さらに踏み込んで考えると、8+3は8+(2+1)に分解できることはわかりましたが、8+2+1とすることも、1+2+8などのように、足し算では数字の順番を変えても答えが変わらないという点を知ることが重要です。このあたりはおはじきを使って視覚的に教えるのも良い方法だと思います。
2桁+1桁の桁上りがない足し算
下記のような足し算です。
| 10 | + | 1 | = | 11 |
| 10 | + | 2 | = | 12 |
| 12 | + | 4 | = | 16 |
| 13 | + | 2 | = | 15 |
| … |
ヒント
この頃になると、数当てゲームやスタンプラリーなどにも慣れてくると思います。
10から99まで全てをやる必要はありません。
合計して100になってしまわないように2桁+1桁の足し算をしていきます。
数をランダムに想像していっしょに計算してみてください。
目標
おはじきや、紙とえんぴつを使って計算をする方法を教えていきましょう。
2桁どうしの繰り上りのない足し算
「12+13=25」のように、足したときに1の位が10以上ににならない2桁の数字の組み合わせの足し算です。これもさくらんぼ計算でも解けますが、この計算からは「筆算」を教えていってください。紙にえんぴつで式を書いて計算する方法です。
「12+13=25」のように、足したときに3桁にならない2桁の数字の組み合わせの足し算です。これもさくらんぼ計算でも解けますが、この計算からは「筆算」を教えていってください。紙にえんぴつで式を書いて計算する方法です。
12 22 18
+13 +32 +41
ーーーー ーーーー ーーーー
25 54 59
のように書いて、1の位どうし、10の位どうしを足せば答えが出せることを教えます。
また、1の位や10の位で繰り上げが発生するかしないかを判断させます。
もしも余裕があれば、桁上がりしない数字である限り1の位どうし、10の位どうしの足し算だけしていけば、下記のような3つや4つの数字の足し算でも(あるいはそれ以上でも)簡単に計算できることを教えても良いです。
12
12 21
21 32
+43 +23
ーーーーー ーーーー
76 88
絶対にやらないでほしいこと
計算問題をたくさん用意しておいて、自習させ、自分は家事をするために席を立つというのは絶対にやめてください。家庭での「べんきょう」は親子の共同作業です。
ヒント
問題をいっしょに作ることをしてください。
答えを考えるだけでなく問題も考えることは重要なことです。
繰り上がりが無い場合は、単純な1桁の数字の足し算に似ていることを発見できたら褒めてげましょう。
目標
筆算で2桁の繰り上がりしない数字の足し算がすらすらできるように練習しましょう。
コラム:答えではなく、問題を考える意味
小学校から高校までの「勉強」は、
与えられた「問題」に対して「答えを出す」ことがすべてです。
しかし、大学以降で行う本来の「学問」とは「問いを学ぶ」ことです。
すなわち
「問いそのものを考え、その答えを自らの努力で探す」
「そもそも何を問うべきか」、「何がわかっていないのか」を自分で発見する。
そのことこそが真の学問なのです。
2桁どうしの繰り上がりのある足し算
これがマスターできれば、あとは3桁でも4桁でも計算できるようになるはずです。
筆算の練習と「繰り上がり」の見える化:38+27
やはり算数をレベルアップするには筆算を避けて通れませんので、ここで筆算をたのしみながら勉強していくと良いと思います。
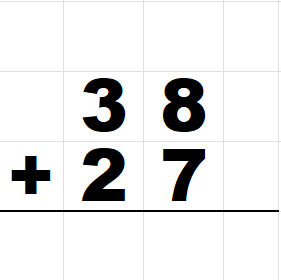
38+27の足し算を考えてみます。
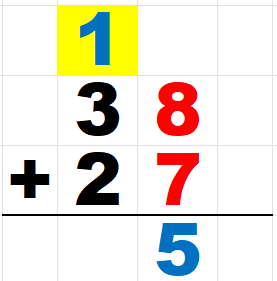
1の位(8と7)を足し算します。
答えは15なので、10の位に1を積みます。

10の位の数字(1と3と2)をすべて足し算します。
1+3+2=6
10の位は6です。
並べて書くと65
答え:65
100の位へ繰り上がる場合の計算:89+34
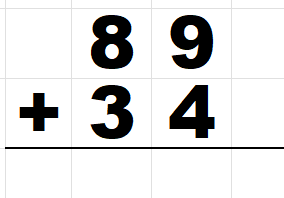
100の位でも繰り上げがある計算です。
89+34
これも理屈はまったく同じです。
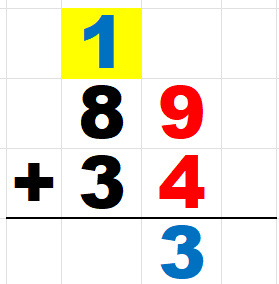
まず1の位(9と4)の足し算をします。
9+4=13
10の位に1を繰り上げる。
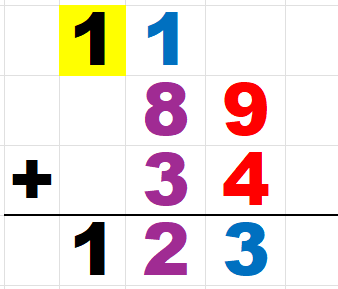
10の位(1と8と3)をすべて足すと、
1+8+3=12
10を超えているので100の位へ繰り上げる。
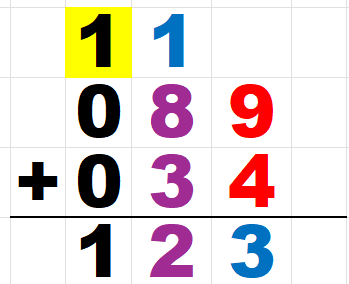
100の位は、右の図のように
089と
034と見ても良い。
その場合1+0+0となるので分かりやすい。
ヒント
筆算の練習は、色ペンなどを使ってカラフルに描いたりすると、楽しく勉強できる。
こどもが、2桁の計算をさくらんぼ計算に応用できたりしたら、大いに褒めてあげましょう。
気づきを褒める
ここでもやはり子供の「気づき」を大切にしてください。
例えば、2つの2桁の数字の足し算であれば、絶対に桁上がりで繰り上がる数字は「1」しかない
などです。
大人にとって当たり前のことでも、
その子供がはじめて気づいたことならば誉めてあげてください。
目標
桁数の多い足し算でも筆算を駆使して計算できるようになる。
カラフルに筆算をしよう

色をつけながら勉強するのに最適:
クーピーペンシル。
https://amzn.to/4kgMV2d
効果的なメモの取り方
ノートにメモを取るのも良いのですが、教える科目やトピックが変わってしまうと、同じノートにメモを書くことは現実的でなくなることが多いです。
京大カードのおすすめ
京大カードというのを聞いたことがあるでしょうか?
元京都大学名誉教授の故梅棹忠夫先生が考案したパソコンもワープロもなかった時代の「情報を効率よく整理する」ための方法です。
アマゾンで購入することもできます。



使い方
・1枚のカードには1つのトピックのみを書く。
・左上の四角欄に「さんすう」「りか」などのカテゴリ名を書いておく
・一番上の欄には「タイトル」を大きく書いておく
・欄外に最初に作成した日付、その横に後日変更したらその日付を書いておく
➔ カードを専用のB6版のカードが入る箱にすべて入れておく
➔ 調べたいときにはカードのタイトルとカテゴリをざーっとみてカードを場に出しておく
➔ 場に出したカードを読む
基本的に何を書いても良い(絵など入れても色えんぴつを使っても構わない)が、トピックとタイトルだけは共通の書き方にしておいたほうが後で検索しやすい。
さらに高度な方法
同じカードでも20世紀末にドイツのビーレフェルト大学の教授であったニクラス・ルーマンが発案した「ツェッテルカステン」はもう少しシステマチックです。カードに体系的でかつカードごとにユニークなな番号を付与し、カード間のリレーションを番号で管理しようというものです。
ただしこれはちょっと小学生低学年のこどもには難しいので教える必要はありません。
反復学習の重要性とデメリット
人間がものごとを効率よく覚えるために、同じことを何度もする「反復学習」は効果的です。しかし、同じ計算を永遠にやらせてはいけません。飽きて嫌になるだけです。
ゲーム性を大いに取り入れる
本ブログでも紹介してきたような遊びながら学べる工夫を随所に盛り込んでみてください。
とくに親が心の中で思った数字や式を子供に当てさせるゲームなどが喜んで何度でもやりたがるでしょう。こどもが効果的な質問をして、答えにたどり着いたときはよろこびひとしおです。スタンプを余分につけてあげる、嫌いな食材を1回の食事についてだけ食べなくて良い、お菓子を奮発するなど小さなリワード(ごほうび)をあげてください。
ただし金銭をあげる、高価な周遊を約束する、できないことを約束するなどはNGです。
新な発見、難解な問題を解いた、こつこつ努力したときだけ褒める
新たな発見、新しい難問を解いた時だけは盛大に褒めるようにします。
決して多くの問題を解いたからとか、難易度の低い問題をいくつも解いたとか、できてあたりまえの問題で高得点を取ったようなときにおおげさに褒めてはいけません。こどもは親に褒められたい一心で簡単な問題を大量に解こうとして、結果的に学力が低下します。
そのかわりに、新しい発見をしたときや、京大式カードなどをこつこつと作っているとき、新しい問題を自力で解いたとき、難問を解いたときなどは大いに褒めてあげてください。
「数値線」の計算はすごく重要
数値線を使った計算のほうほうをご存じでしょうか?
紙に線を引いてメモリを振り、そのメモリを使って計算を「見える化」する方法です。
これ、この次に出てくる引き算や掛け算などで非常に重要な役割を果たしますので、
いまのうちにしっかり教えておいてください。
数値線
エクセル使っても良いですし、定規で線を引いても構いません。
どんな方法でも良いので0から順番に数字がわかるようにメモリを振っていきます。
エクセルなどで作る場合は、0の位置には「なにもない」ことをわかってもらうために
メモリをつけません。

数値線を使った足し算
8+3を計算してみましょう。
まず数値線上に8をマークします。

メモリの水色の線を数えれば8本あることがわかります。
つぎに、数値線に3を書き足します。
できれば色を変えて、こどもに描かせてみてください。

色鉛筆で線を描くだけで答えが出てしまうことが楽しくて、
何度も数値線の計算をやりたがる子供もいるくらいです。




