人工知能の基礎：パーセプトロン

　人工知能の理解をする第１段階は「パーセプトロン」です。パーセプトロンとは、人工知能や機械学習の基礎となる「人工ニューロン」のモデルの一つです。
　簡単にいうと、「パーセプトロン＝人間の脳の中にある脳細胞（ニューロン）の働きを、すごく簡単な式でマネしたもの」です。これは、1950〜60年代にアメリカの心理学者フランク・ローゼンブラット（Frank Rosenblatt）によって提案された考え方です。

パーセプトロンてなんやねん！？・・・単純パーセプトロンの場合

　もともととっつきにくい単語なので難しく聞こえますが、パーセプトロンとは、簡単に言うと、1本の直線（または1枚の平面）で色のついた赤と黒の点の群れを分けることができる計算モデル（≒関数・モデル）のことを言います。
　このように点の群れをピシッと分けられる性質を『線形分離可能（linearly separable）』と呼びます。
　ちょうど下の図のように赤い点と黒い点が１本の直線でピシッと分けれています。計算の結果赤い点の位置（X=１、Y=１の位置）より上に来たら赤（出力＝１）。線よりも下になったら黒（出力＝０）と分けたります。どっちを赤（１）でどっちを黒（０）にするかは自由に決められます。じつはこれ、人工知能の計算の基本なんです。

2種類のパーセプトロン

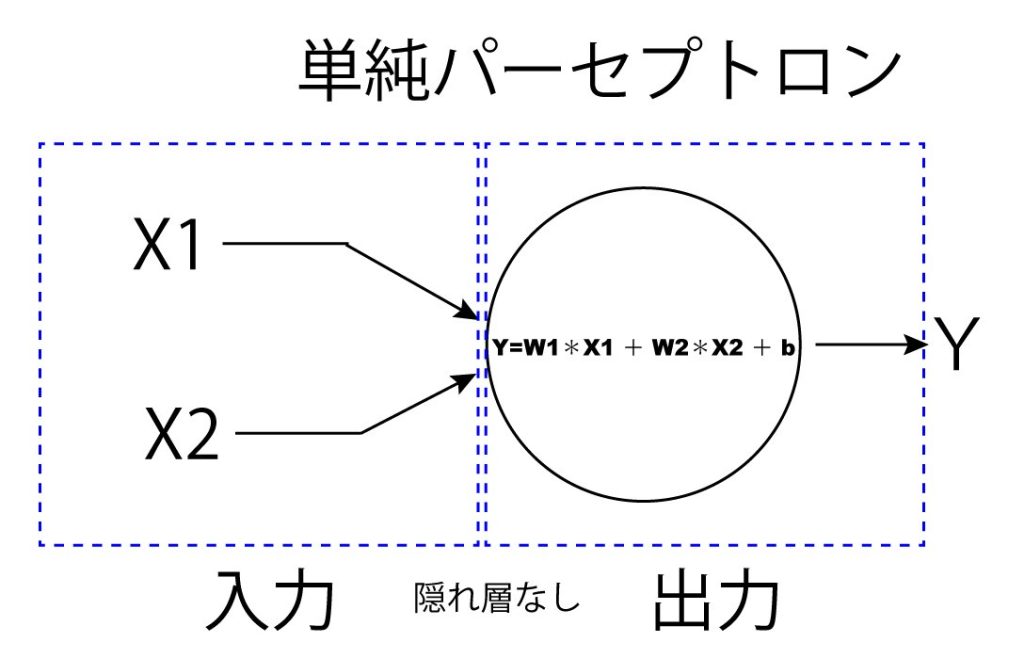
　パーセプトロンは、人工知能を勉強するときにまず理解しないといけない一番の初歩と言いましたが、さきほど説明した線や面で点を分けるのは「単純パーセプトロン」と言います。
　一方でChatGPTなどのように深層学習（ディープラーニング）などで利用されている「多層パーセプトロン（MLP）」と言うのもあります。
　MLPは初心者にはすこし難しい概念なので、本ブログではまず簡単なほうの「単純パーセプトロン」から説明していきます。

実は小学生でもできる単純パーセプトロン

　単純パーセプトロンの代表的な応用方法の１つは、「足し算だけを使って結果を出せる」というだけのことで、小学生でも計算できる単純なものです。

論理演算

　単純パーセプトロンを理解するのに、しばしば利用されるのが「論理演算」です。

論理演算てなんやねん！？

　論理演算といっても方程式を解いたりするわけではありません。表に照らし合わせればいいだけです。計算ですらありません。
　論理演算にはいろいろありますが、主だったものは以下の通りです。

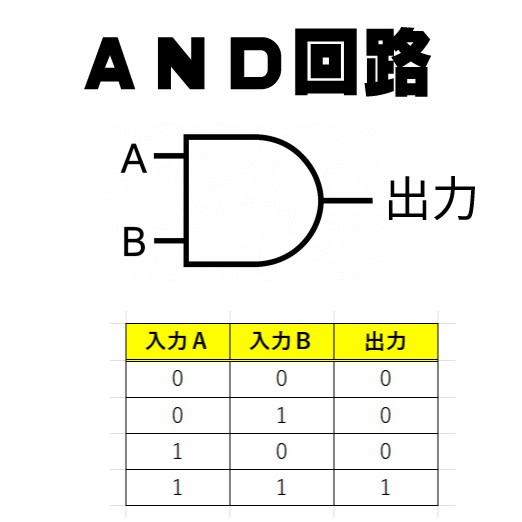
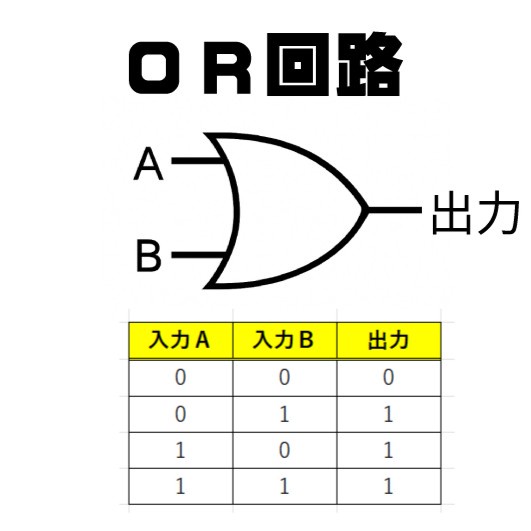
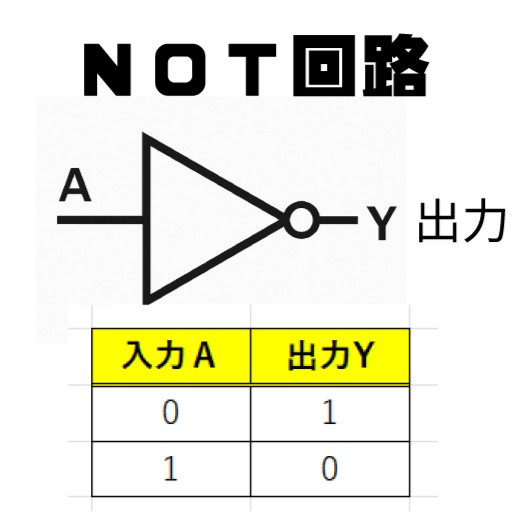
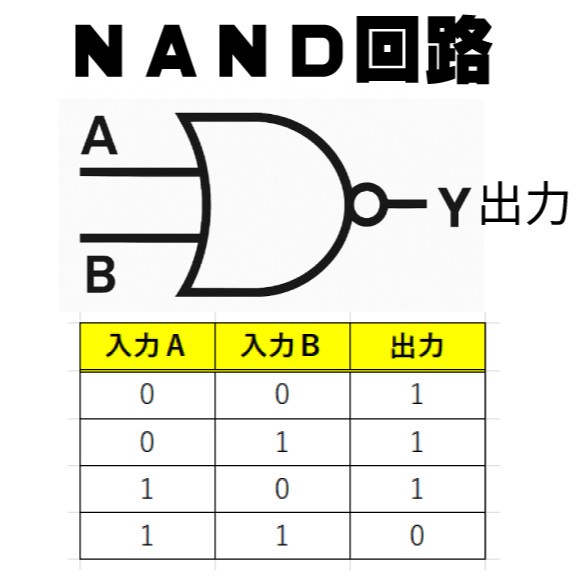
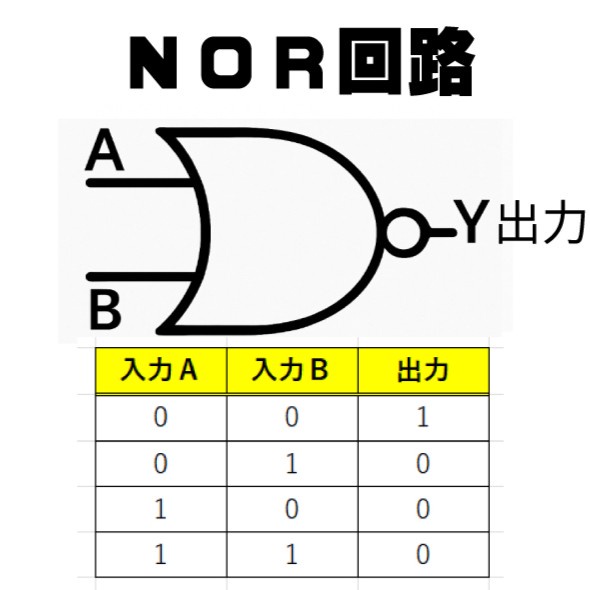
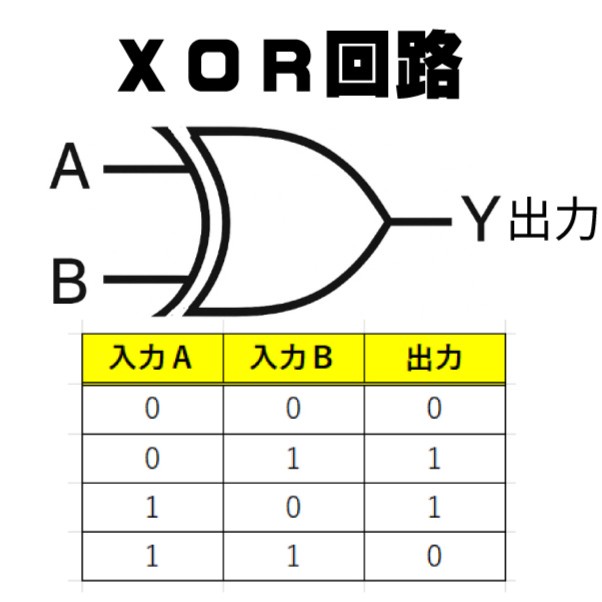
　入力が１個または２個に対して出力（答え）が１個です。入力は電気が来ていたらON（１）、来ていなかったらOFF（０）です。それぞれ表を見ると答えがわかります。
　入力のAとBが両方ともON(１）のときだけ出力がON(１）になるのがANDといいます。同様に入力のAとBのどっちかがON（１）だったら出力もON（１）となるのがORです。

　この論理演算はコンピュータの命令１発で計算できてしまうのですが、これをパーセプトロンを使ってやってみるというのが人工知能の「パーセプトロン」を理解する第１歩です。

グラフを使って論理計算の答えを出す

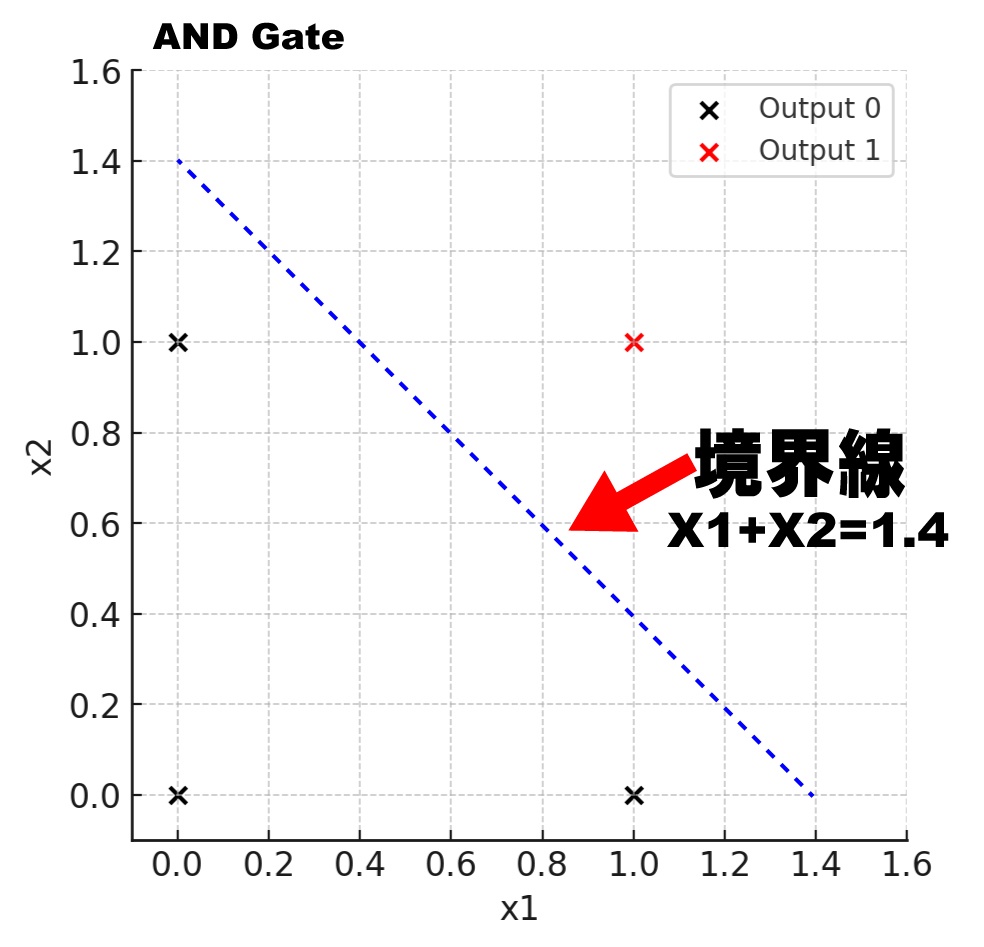
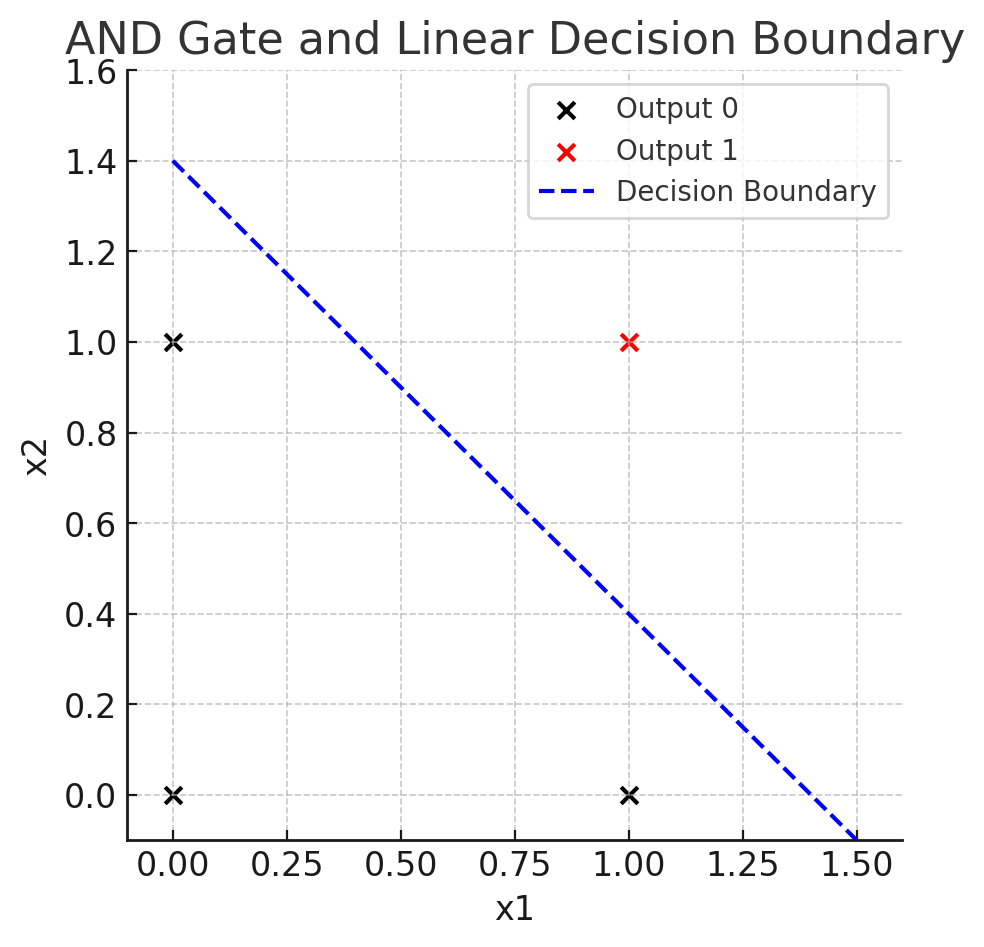
　ANDゲート（回路）は２つの入力が両方ともON(1）のときだけ出力をON（１）にできれば良いんでしたよね？　ここでは例として入力ＡをＸ軸、入力ＢをＹ軸とすることにします。
　そこでＡＮＤゲート（回路）の計算をグラフに書いてみると、ＸとＹが両方０の地点では黒（ＯＦＦ）ですね、同様にＸ軸とＹ軸の値が［１，０］と［０，１］のときも黒（ＯＦＦ）で、唯一ＸとＹが両方とも１のときだけ答えがＯＮ（１）になることが視覚的にわかると思います。
　単純パーセプトロンは、これらの赤と黒の点の群れたちをピシっと直線で分けられればいいんですよね？
　それをするには、Y軸の1.4からX軸の1.4とか、Y軸の1.５からX軸の1.５あたりへ向かって直線を引くと、ちょうど赤の点と黒の点を分離できますよね。

パーセプトロンの計算式

　これは、パーセプトロンの「境界線（決定境界）の方程式（equation）」と言い、さきほどのグラフのような境界線を引くための計算式です。W1 x X1 + W2 x X2 + b が０以上か、０以下かで判断します。

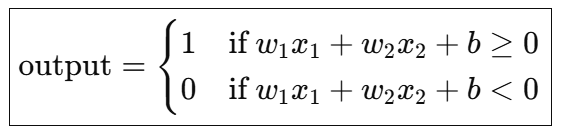
　これをＡＮＤの表（Ｙ軸Ｘ軸ともに１．４のところを結んだ線を出す式から導いてみます。

境界線の式

　Ｘ軸、Ｙ軸それぞれ1.4のところを結んだ線を引くので、この傾きを表す式は、

Ｙ＝ーＸ ＋ １．４

　境界線が右下がりなのでマイナスＸになりますね。
　ここからパーセプトロンとして機能するように式を書いていきます。
パーセプトロンの式の形は・・・

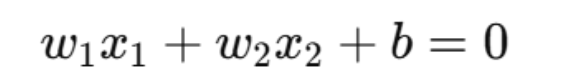
これにはじめに設定したX1をY、X2をXにしていたんで、元に戻して今回の傾きの式を当てはめると、
「Y = -x + 1.4 」➔ この式を全部左辺に寄せると
「Y+X-1.4=0」➔ パーセプトロンの式にあてはめると…
「A + B -1.4 => 0」のときだけ真（１：ON）になります。

サンプルプログラム

なんでちがう？

　TOUの人工知能演習では下記のように 「0.5×1 + 0.5×2 -0.7 >= 0」 のみが正解でしたね？

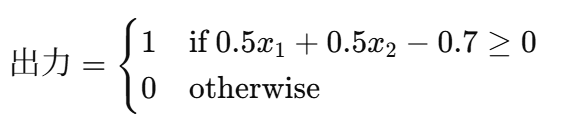
そして小テストの正解として以下のプログラムが掲載されていました

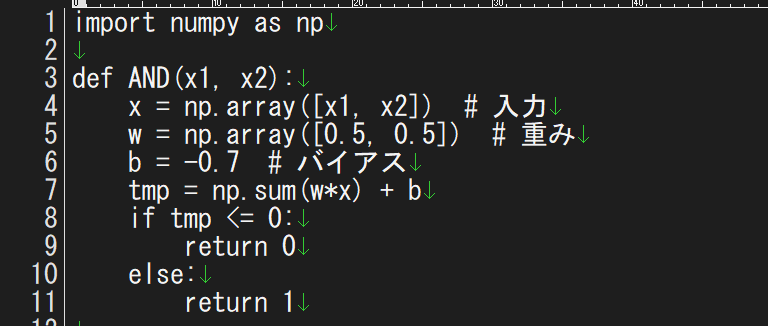
なんでそうなるのか・・・
答えは簡単です。
「人工知能演習で使っている参考書がそうなっているから」です💦
本来は、x1 + x2 – 1.5 でも x1 + x2 -1.45 でもいいんです。
赤い点だけがグラフの斜線の上に出れば良いのですから。

参考書は買っておいたほうが良い

その他の論理回路も全部おなじりくつで計算できる

XORだけ特別

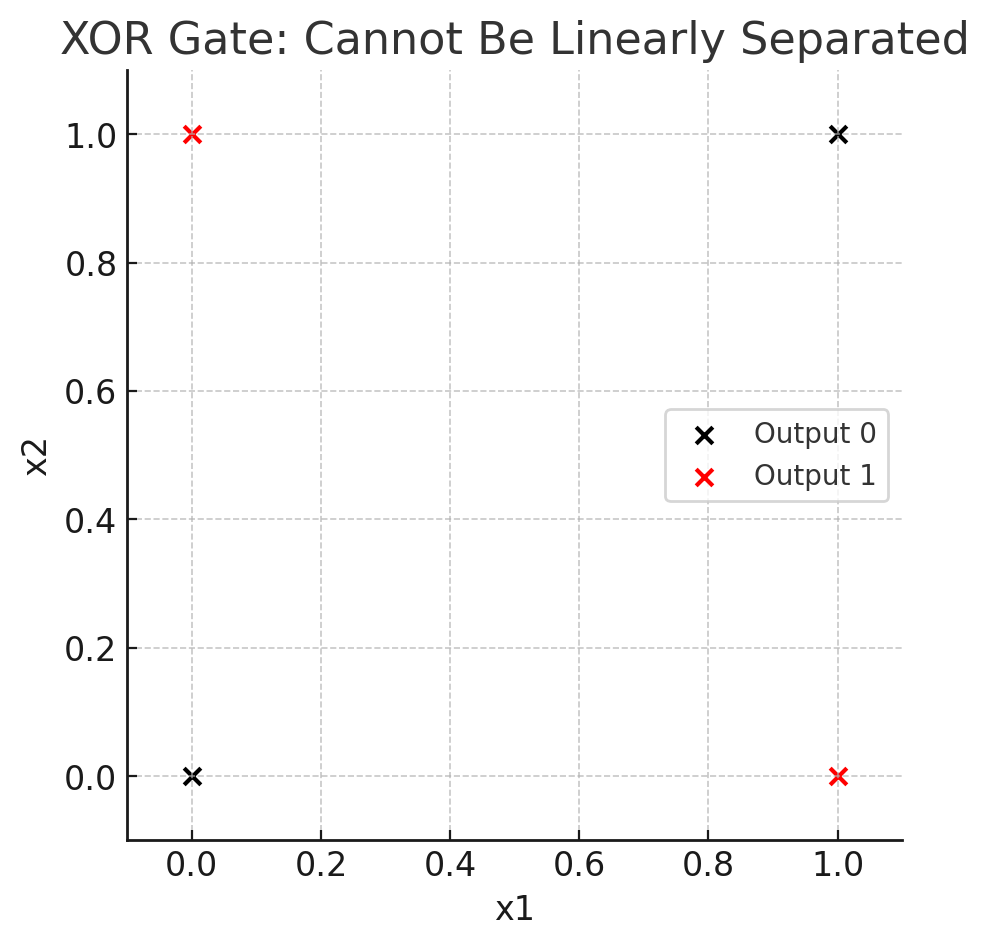
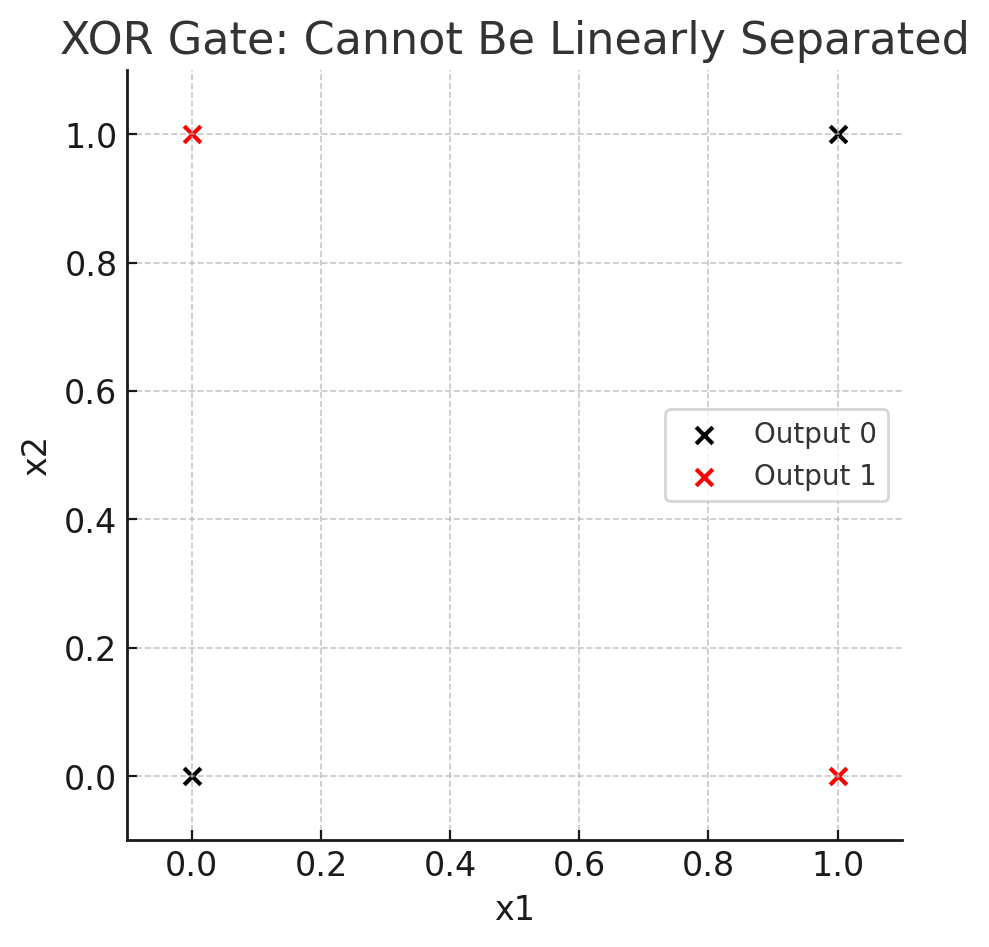
　しかしこれも後で詳しく説明しますが、XOR（排他的論理和）だけは、下のグラフでもでわかるように、出力０の点（黒い点）と出力１の点（赤い点）を直線で分けることができない（線形計算できない）ので、単純パーセプトロンでは解を求められません。このことは後で詳しく解説します。

単純パーセプトロン

　さて、入力部と出力部しか無く、論理演算を足し算だけでやってしまおうという場合の単純パーセプトロン、実際にAnacondaのJupitar Note （Python）を使ってやっていきましょう。

ANDの解を単純パーセプトロンで出す

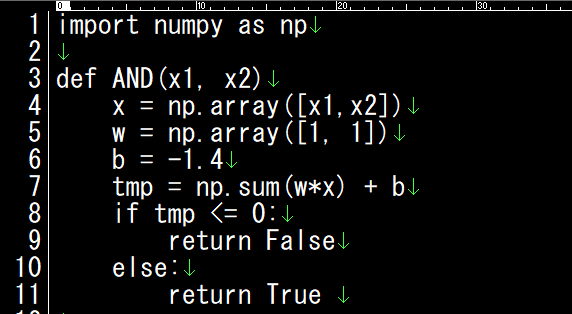
　下記はパーセプトロンを使ったANDゲート（回路）の計算をpython言語とnumpyライブラリをimport文を使って導入して解いてみるプログラムです。ぱっと見ると難しそうですが、１行づつ見ていくと、とても簡単な処理しかしていないことが分かります。

プログラムを読み解く

行数	プログラム
１	numpyライブラリを読み込む命令です
2	ANDを計算する関数の定義です
3	C言語風に書くと➔のようになります	double x[2] = {x1, x2};
4	これもC言語風に書くと➔になります	double w[2] = {0.5, 0.5};
5	ｂは調整値	-0.7
6	この計算は単純に書くと➔のようになる	double sum = w[0] * x[0] + w[1] * x[1] + b;
７～10	ここで６行目の計算結果がゼロかマイナス なら「０」を出力し、そうでなければ 「１」を出力しています。
12～15	定義したAND関数に、それぞれ （0,0）（0,1）（1,0）（1,1） を引数として渡して、その結果を画面に 表示する処理です。

　結局いろいろ難しそうに見える命令がでてきますが、実際にやっていることが単純な配列を使った足し算だけなのがわかったと思います。

計算してみる

　つまりこのPythonで書かれたANDゲート（回路）関数は、X1（＝入力A、X軸）とX2（＝入力B、Y軸）という２つの入力をとり、以下のように計算して答えを出すという単純なものです。
　　AND= X1＊0.5 + X2*0.5 ＋（-0.7）
もちろん
　　AND=x1 * 1 + x2 * 1 + (-1.4)
でも良いんです。
この解がプラス（境界線より上）なら出力は１、マイナス（境界線より下）なら出力は０ということになります。

境界線を引く

これをグラフにプロットするために境界線の式を求めるには以下のようにします。
まず、基本の式：（w1*x1）＋（w2*x2）＋ｂ＝０にあてはめて考えます。
①　　( 0.5 * X1 ) + ( 0.5 * X2 ) -0.7 = 0
①の両辺に+0.7を足して左辺から-0.7を削除して②を得る
②　　( 0.5 * X1 ) + ( 0.5 * X2 ) = 0.7
②のすべての項を２倍して0.5を消して③を得る
③　　X1 + X2 = 1.4
ここで、
X1（X軸）が０のとき、X2（Y軸）は1.4、
X2（Y軸）が０のとき、X1（X軸）は1.4、
となるので、X軸の1.4 からY軸の1.4を線で結べば「ANDの境界線」が引けます。

　境界線の上にでた赤い点（座標でいうとＸ軸とY軸の値が両方とも１の点）だけが「１」を出力するということがわかると思います。

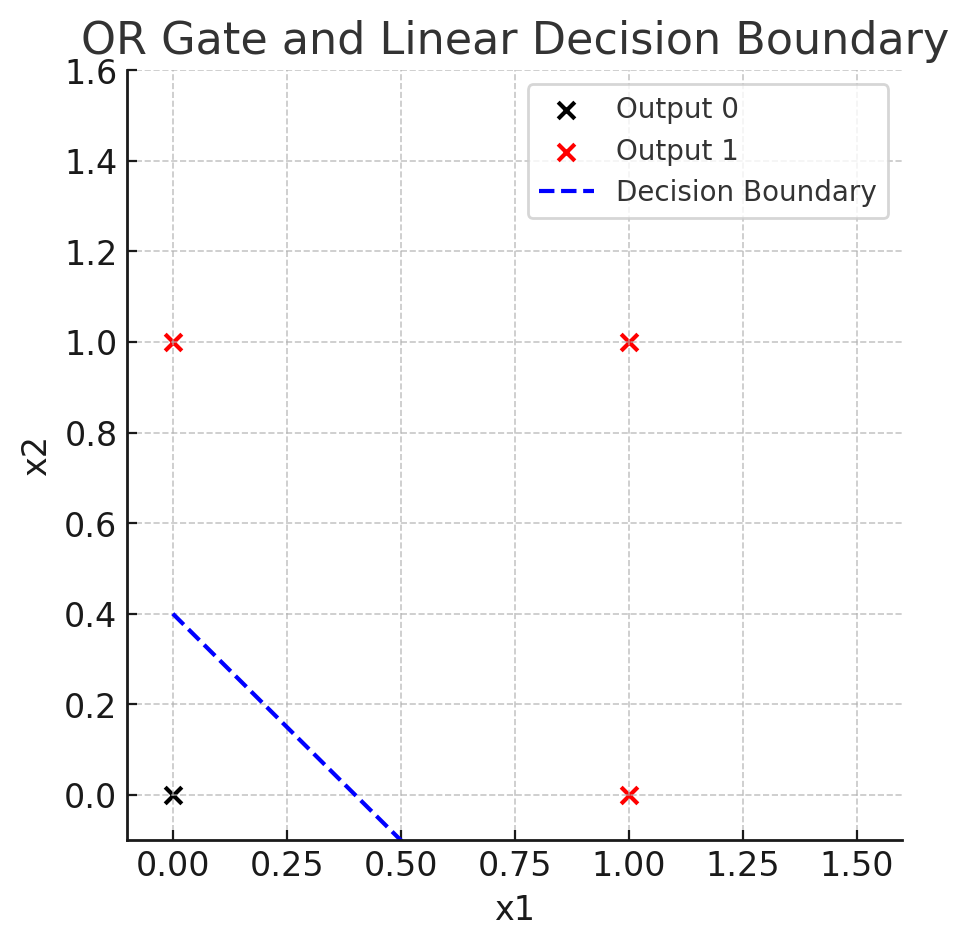
ORの場合もおなじにできる

　論理演算「ORゲート（回路）」の場合も見ていきましょう。ORゲート（回路）はAとBの入力が両方とも０でない限り「１」を出力する論理演算です。

ORのグラフ計算

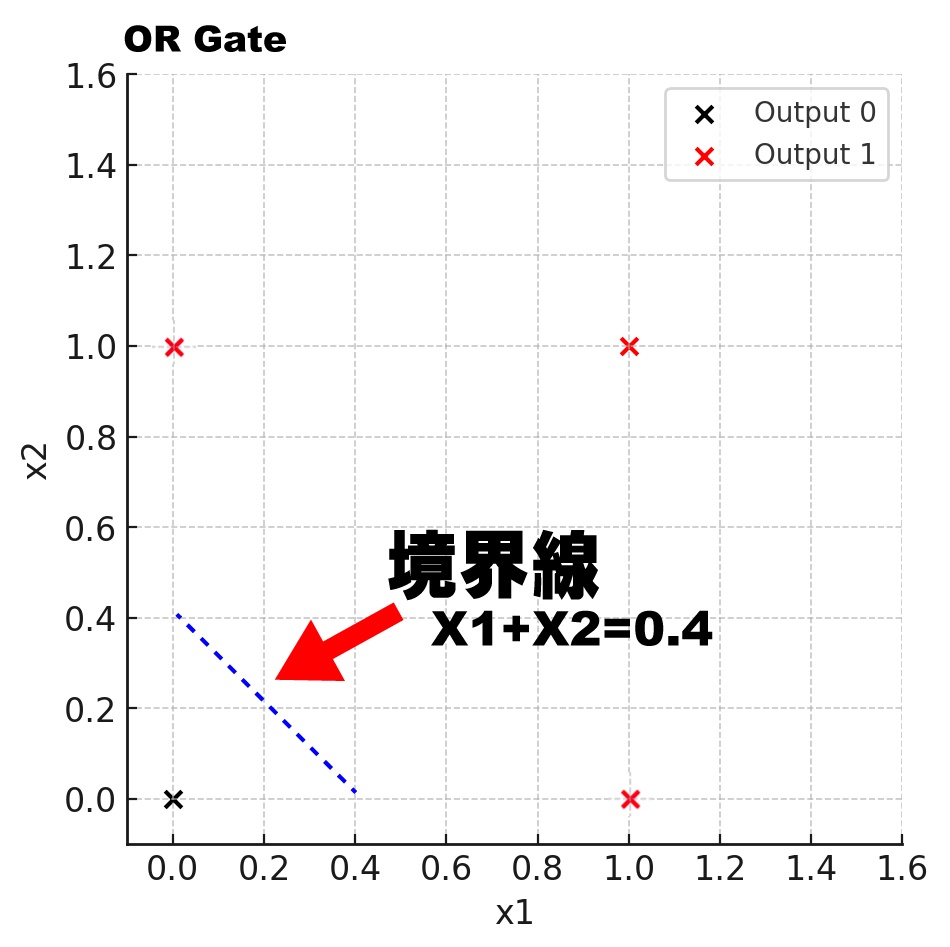
　ORの場合は、境界線をずらしてX1とX2が両方０でないとき以外はすべて境界線の上側に出るように線を引いてあげればいいわけです。ORをグラフで計算するには、バイアス値（またはしきい値と呼ぶ）「ｂ」の値をずらすだけでカンタンに実現できます。

　先ほどと同じように境界線の式を見てみると、以下のようになります。
　これをグラフにプロットするために境界線の式を求めるには以下のようにします。

まず、基本の式：（w1*x1）＋（w2*x2）＋ｂ＝０にあてはめて考えます。
①　　( 0.5 * X1 ) + ( 0.5 * X2 ) -0.2 = 0
①の両辺に+0.2を足して左辺から-0.2を削除して②を得る
②　　( 0.5 * X1 ) + ( 0.5 * X2 ) = 0.2
②のすべての項を２倍して0.5を消して③を得る
③　　X1 + X2 = 0.4

この計算結果をもとに、
X1（X軸）が０のとき、X2（Y軸）は0.4、
X2（Y軸）が０のとき、X1（X軸）は0.4、
となるので、X軸の0.4 からY軸の0.4を線で結べば「ORの境界線」が引けます。
もちろんORゲート（回路）も x1 + x2 -0.4 でも、x1 + x2 -0.6 でも、x1 + x2 -0.8 でも答えは同じになります。
ではなんで x1 * 0.5 + x2 * 0.5 – 0.2 なのかと言えば、
先ほどと同様に「参考書がそうなっているから」です💦
実際は結果さえ合っていれば、どんな値をとってもOKです。

プログラム

ORの場合はバイアス値（ｂ）の値が変わっただけでほかはANDと全く同じ処理をしています。

NOTつきの回路の場合は？

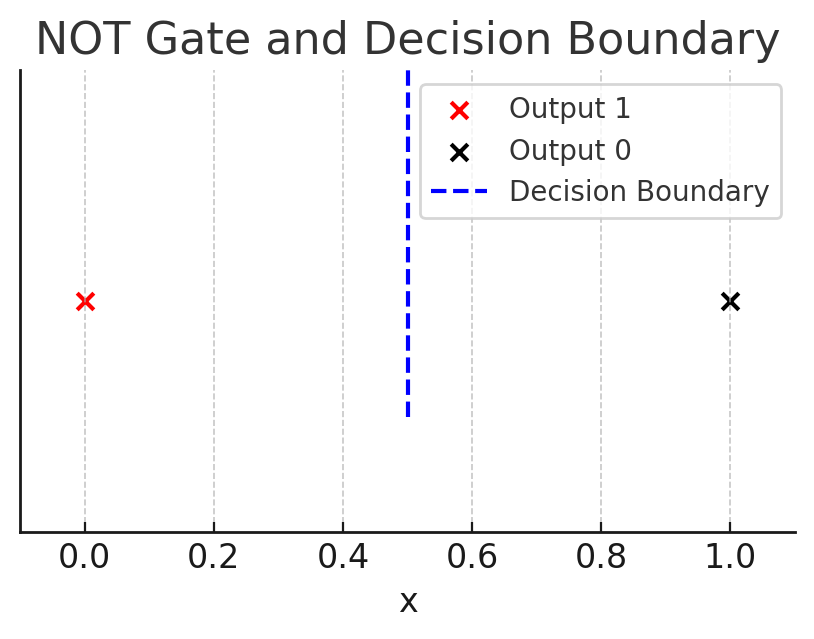
　論理回路にはNOTという入力値と逆の値を出力するものがありますが、ANDやORをこのNOTと組み合わせて、NANDゲート（回路）、NORゲート（回路）として使うことがあります。

　NANDゲート（回路）やNORゲート（回路）などの論理演算も、単純パーセプトロンでマネすることができます。やりかたは、グラフの見方を逆にして境界線の下側に出たら１を出力すれば良いのです。これを実現するのは簡単で、たとえばNANDの場合は、
　　( -0.5 * X1 ) + ( -0.5 * X2 ) + 0.7 = 0
というようにパラメータの正負を逆転させれば良いのです。

グラフで計算

　線形計算（グラフで計算）する場合、境界線はANDゲート（回路）のグラフの境界線と同じですが、NANDゲート（回路）の場合は、境界線の下側に入ったときに１を出力します。

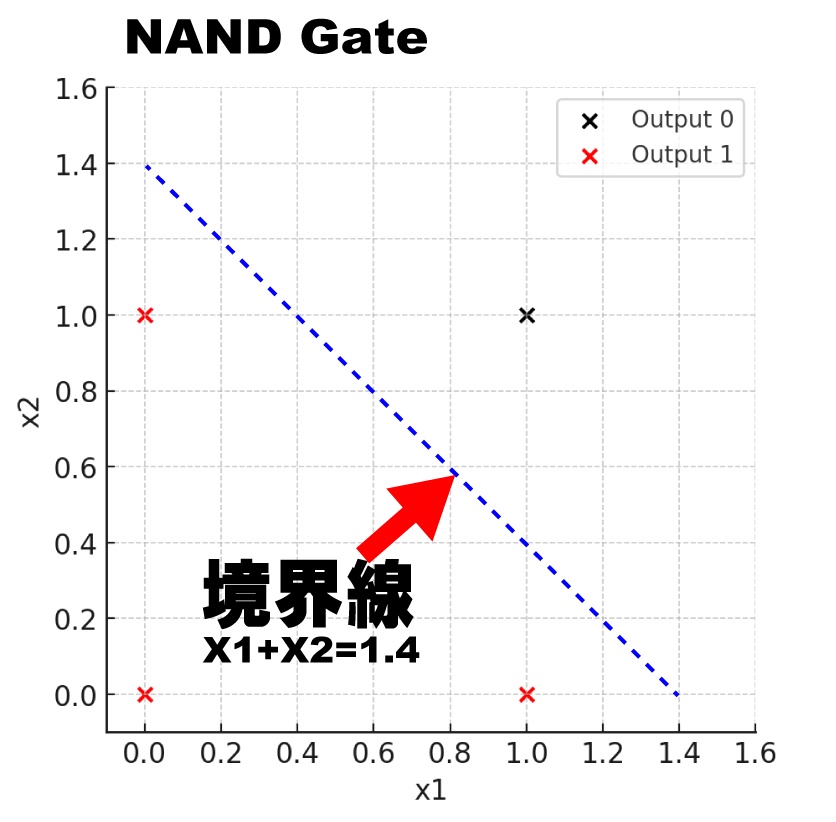
　パラメータの正負を反転させて、境界線の下に出た点を赤（出力が１）の点にするわけです。

プログラム

　プログラムもANDゲート（回路）とほぼ同じで、違うところは数値の符号が正負逆転していることだけです。この理屈はORゲート（回路）の場合もまったく同じです。

異端児ＸＯＲ

　今までは単純パーセプトロンの考え方を使って論理演算をまねする場合にグラフで直線を引くか、かんたんな足し算をすればよかったのですが、排他的論理和（ＸＯＲゲート（回路））だけはこのやり方では答えが出せません。１本の直線でこの２つの赤（出力が１になる点）と２つの黒（出力が０になる点）を分離できないからです。こういう計算のことを「非線形計算」といいます。

ではそどうやって計算する？

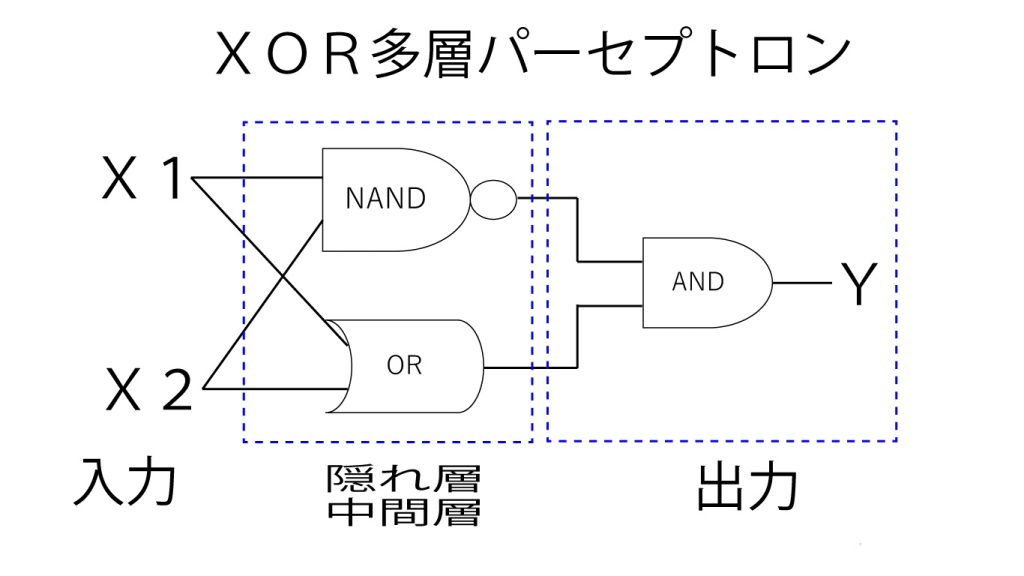
　ここで多層パーセプトロン（MLP）の登場です。多層パーセプトロンとは、入力と出力だけしかない単純パーセプトロンと違って、その内部に「隠れ層」と呼ばれる計算処理を入れてあるパーセプトロンのことです。XORゲート（回路）の計算をこの多層パーセプトロンの考え方で解くには、以下のような構造が必要になります。こうすることで上の真理値表の通りになるのが分かると思います。

プログラム

　プログラムはいたってカンタン！ NAND,OR,ANDをそれぞれ組み合わせるだけです。

図で描くと難しそうに見えますが、プログラムで書くとめちゃくちゃカンタンになりますね。しかもちゃんとXORの結果がでます。